Getting Calvin home on time: a statistics puzzle

Posted on Thu 19 July 2018 • 10 min read

I found this puzzle a while ago and couldn’t get it out of my head, so I decided to write up a solution.

Calvin has to cross several signals when he walks from his home to school. Each of these signals operate independently. They alternate every 80 seconds between green light and red light. At each signal, there is a counter display that tells him how long it will be before the current signal light changes. Calvin has a magic wand which lets him turn a signal from red to green instantaneously. However, this wand comes with limited battery life, so he can use it only for a specified number of times.

a) If the total number of signals is 2 and Calvin can use his magic wand only once, then what is the expected waiting time at the signals when Calvin optimally walks from his home to school?

b) What if the number of signals is 3 and Calvin can use his magic wand only once?

c) Write a program that takes as inputs the number of signals and the number of times Calvin can use his magic wand, and outputs the expected waiting time

Assuming that the lights are independent, the time until a light changes (displayed on the counter) when Calvin arrives is drawn from a uniform distribution between 0 and 80:

$$ t_{\text{counter}} \sim \text{Unif}(0\ \text{s},80\ \text{s}).$$

So the average waiting time at each red light is 40 seconds. Since there is a 50% chance that the light is green, the expected waiting per light time is

$$ \bar t_{\text{wait}} = P(\text{green}) \cdot \bar t_{\text{counter}} = \frac{1}{2} \cdot 40\ \text{s} = 20\ \text{s}. $$

Calvin wants to use his wand in order to minimize his waiting time.

a) If the total number of signals is 2 and Calvin can use his magic wand only once, then what is the expected waiting time at the signals when Calvin optimally walks from his home to school?

With two lights and one use of the magic wand, there are three scenarios that can arise:

If the first light is green (50% chance), then Calvin will use his wand on the second light, with 0 waiting time.
If the first light is red (50% chance):
- He will use his wand if the time on the timer is higher than the expected wait for the second light (20 seconds, 75% chance). In this case the expected waiting time is the expected time for the second light: 20 seconds.
- He will not use his wand if the time on the timer is less than 20 seconds (the mean time these cases is 10 seconds since they are uniformly distributed between 0 and 20, and the situation occurs with a 25% chance). In that case he will wait, and use his wand on the second light, for a total expected waiting time of 10 seconds.

His total expected waiting time is found by taking a sum of all the different situations weighted by their probability:

$$ \bar t_{wait} = 0.5 \cdot 0\ \text{s} + 0.5\cdot(0.75 \cdot 20\ \text{s} + 0.25 \cdot 10\ \text{s}) = 8.75\ \text{s}$$

So Calvin’s expected waiting time is 8.75 seconds.

Let’s confirm this by trying it… one billion times [evil laugh]:

import numpy as np

n_trials = int(1e9)

# initialize the trials
wait_times = np.zeros(n_trials)

# light waiting times: uniform 0-80 seconds, 50% chance of being green (0 wait time)
t1 = np.random.uniform(0, 80, n_trials) * np.random.randint(0, 2, n_trials)
t2 = np.random.uniform(0, 80, n_trials) * np.random.randint(0, 2, n_trials)

wand1 = (t1 >= 20) # trials where Calvin uses the wand on light 1

# wait at light 2 wherever he uses the wand at light 1
wait_times[wand1] = t2[wand1] 
# wait at light 1 wherever he doesn't use the wand at light 1
wait_times[~wand1] = t1[~wand1]

print('Calvin\'s mean waiting time in {:,} trials was {:.3f} seconds'\
      .format(n_trials, wait_times.mean()))

Calvin's mean waiting time in 1,000,000,000 trials was 8.750 seconds

Nice!

b) What if the number of signals is 3 and Calvin can use his magic wand only once?

Now we have three signals and one wand usage. Since we have one wand, we want to find some optimal cutoff value that lets us decide whether or not to use the wand at each light. We base this on whether or not we expect to see a light with a higher waiting time than the current counter during the rest of our walk home.

At the last light, the cutoff is zero. If we haven’t used the wand yet, we will definitely use it if the light is not green, as there are no more chances left to use it.

We’ve already shown that the cutoff at the second-to-last light should be 20 seconds, as this situation is the same one as in part a) (assuming the wand hasn’t been used yet).

What about at the first light? We want to know the expectation value of the maximum of the next two waiting times.

The probability that the counter displays a waiting time is less than some time $t$ is given by

$$ \tilde{F}(t) = P(t_{\text{count}} \le t) = \frac{t}{80}. $$

$\tilde{F}(t)$ here is the Cumulative Density Function (CDF) for our uniformly distributed counter time.

Now, there is a 50% chance that the light will be green, in which case our waiting time is zero, regardless of the value displayed on the counter. This means that the probability of the waiting time being less than or equal to zero is already $1/2$, and it grows linearly to $1$ for a waiting time up to $80$ seconds. So including the chance of a green light, the CDF for our waiting time is

$$ F(t) = P(t_{\text{wait}} \le t) = \frac{1}{2} + \frac{1}{2}\frac{t}{80} .$$

We are interested in the maximum expected waiting time for the last 2 lights in Calvin’s journey, so that he knows what his cutoff should be at the first light. What is the relevant CDF? If the maximum of two random variables is less than a time $t$, then each of the variables must be less than $t$ individually. Since we are assuming that the waiting times are independent, their probabilities factor, and we get the CDF

$$ F_2(t_\max) = P(t_{\text{wait},1},t_{\text{wait},2} \le t_\max) = P(t_{\text{wait},1}\le t_\max)P(t_{\text{wait},2} \le t_\max) = F(t_\max)^2. $$

Clearly this generalizes to $n$ remaining lights, so let’s consider the more general case and then specify $n=2$ to get the cutoff we want. We have

$$ F_n(t_\max) = F(t_\max)^n = \left( \frac{1}{2} + \frac{1}{2}\frac{t_\max}{80} \right)^n. $$

We are looking for the expected value of this maximum. The expectation can found directly from the CDF by

$$ E_n = 80 - \int_0^{80}\!\! \text{d}t\ F_n(t) = 80 - \int_0^{80}\text{d}t \left( \frac{1}{2} + \frac{1}{2}\frac{t}{80} \right)^n$$

(this can be seen from integrating the normal definition, $E = \int \text{d}x\ x\ \text{PDF}(x)$, by parts). To take the integral, we perform the substitution $u = 1/2 + t/(2\cdot80)$ and get

\begin{align*} \int_0^{80}\text{d}t \left( \frac{1}{2} + \frac{1}{2}\frac{t}{80} \right)^n &= 80 \cdot 2 \int_{\frac{1}{2}}^1 \text{d}u\ u^n \\ &= 80 \cdot 2 \left. \frac{u^{n+1}}{n+1} \right|_{\frac{1}{2}}^1\\ &= 80 \cdot \frac{2}{n+1}\left(1-\frac{1}{2^{n+1}}\right). \end{align*}

Inserting this result into our expression for the expected maximum, we get

$$ E_n = 80 \cdot \left(1 - \frac{2}{n+1}\left(1-\frac{1}{2^{n+1}}\right)\right) = 80 \cdot \left(\frac{n}{n+1} - \frac{1}{n+1}\left(1-\frac{1}{2^{n+1}}\right)\right). $$

Interestingly, in the second form above, $80\cdot n/(n+1)$ is the expected maximum waiting time if we had to wait at every light, and the second term is a correction due to half of the lights being green. Again we can confirm our calculation by simulation:

import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')

# simulate (up to) 25 lights
n_lights = 20
n_trials = int(1e7)
counter_max = 80

# simulate the lights (one row per light, one column per trial)
trials =  np.random.uniform(0, counter_max, (n_lights, n_trials,))\
            * np.random.randint(0, 2, (n_lights, n_trials,))

# get the max waiting times for each possible number of lights
t_max = np.zeros(trials.shape)
for i in range(n_lights):
    t_max[i, :] = trials[:i+1, :].max(0)

# get the calculated expectation and simulated mean of the max waiting times
n = np.arange(1, n_lights+1)
wait_max_exp = counter_max * (1 - (2/(n+1))*(1 - 1/(2**(n+1))))
wait_max_sim = t_max.mean(1)

# plot to compare
plt.figure(figsize=(12, 5))
plt.scatter(n, wait_max_exp, s=65, marker='x', c='b', label='expectation')
plt.scatter(n, wait_max_sim, s=35, alpha=0.7, c='r',
            label='simulation ({:,} trials)'.format(n_trials))
plt.xticks(n); plt.xlabel('Number of lights')
plt.ylabel('Max waiting time (seconds)')
plt.xlim([0, n_lights+1]); plt.ylim([0, counter_max])
plt.title('Maximum expected waiting time in sample of $n$ lights')
plt.legend();

png

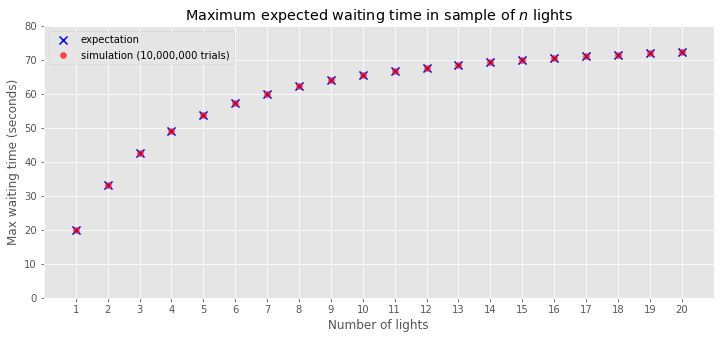
So we have values to function as our cutoffs, based on how many lights are remaining in the journey. Specifically, the cutoff for the first of 3 lights is given by the maximum expected wait time for the remaining $n=2$ lights:

print('Max expected waiting time for 2 remaining lights is {:.2f} seconds.'\
      .format(wait_max_exp[1]))

Max expected waiting time for 2 remaining lights is 33.33 seconds.

Calvin should use his wand if the first light is red and the counter is over 33.33 seconds. We can calculate his expected waiting time by using the result from a) and considering the possible scenarios:

The first light is green (50% chance). In this case Calvin has two lights and one wand to go; this is the situation from a). In this scenario the expected waiting time is 8.75 seconds.
The first light is red (50% chance):
- The timer is over the cutoff ( $(80-33.33)/80 = 58$% chance for uniformly distributed time on the counter). In this case Calvin uses the wand, and with no wands left he expects to wait for 20 seconds per light for the remaining number of lights. There are two lights left, so the expected wait time in this case is 40 seconds.
- The timer is under the cutoff (42% chance). In this case Calvin waits for the displayed time (expectation $33.33/2 = 16.67$ seconds) and then moves on to the situation in a) for a total expected waiting time of $16.67 + 8.75 = 25.42$ seconds).

Again we find his total expected waiting time by taking the weighted sum:

$$ \bar t_{\text{wait}} \approx 0.5 \cdot 8.75\ \text{s} + 0.5 \cdot \left(0.58\cdot 40\ \text{s} + 0.42 \cdot 25.42\ \text{s} \right) \approx 21.3\ \text{s}$$

Note that this by-hand calculation has some rounding errors in the cutoff and proportions, but the exact value also rounds to 21.3 seconds.

c) Write a program that takes as inputs the number of signals and the number of times Calvin can use his magic wand, and outputs the expected waiting time

Now we want full generalization to any number of lights and wand uses. It should be clear from the reliance of the calculation in b) on the results from a) that we can use a recursive strategy to calculate the total waiting time.

There are two questions to answer: What should the cutoff be for multiple uses of the wand? And what is the recursive pattern for calculating the expected wait time?

Let’s begin with the cutoff. When Calvin comes to a red light, he must decide whether to use the wand or not. For a walk with $n$ lights, our strategy has been to consider the expected maximum wait encountered during the next $n-1$ lights. We can generalize by considering the expected maximum wait at the number of remaining lights we expect to wait at, including the current one. If Calvin has $w$ uses of his wand, then he can skip up to $w$ lights, meaning he has to wait at $n-w$ lights in total, including the current one. So the cutoff for using the wand can be generalized to

$$ E_{\tilde{n}} = 80 \cdot \left(1 - \frac{2}{\tilde{n}+1}\left(1-\frac{1}{2^{\tilde{n}+1}}\right)\right),\ \tilde{n} = n - w. $$

This new cutoff is smaller than the previous one when $w>1$, which makes sense since we would then like to be more liberal with our wand usage.

Now that we have the cutoff, we need the recursive pattern. Again we have three scenarios. If we have $n$ lights and $w$ wands to go, then the scenarios are:

The current light is green (50% chance). In this case the expected waiting time is just the waiting time for $n-1$ lights and $w$ wand uses.
The current light is red (50% chance):
- The waiting time is below the cutoff (probability $\text{cutoff} / 80$). In this case Calvin doesn’t use the wand, and the total waiting time is the wait at the current light (expectation $\text{cutoff}/2$) plus the expected wait at $n-1$ lights with $w$ wands.
- The waiting time is above the cutoff (probability $1 - \text{cutoff} / 80$). Now Calvin uses the wand, adding no extra waiting time, so the expected total wait is the expected wait for $n-1$ lights and $w-1$ wands.

We calculate these scenarios, recursing whenever we need a new total expected wait time for a different number of lights and/or wands, until we hit one of the base cases. There are a few:

If we have 0 lights to go, then the expected total remaining wait time is 0 seconds.
If the number of wands is greater than or equal to the number of lights, then the wait time is 0 seconds (since we can switch all the lights off).
If we have no wands left, then the wait time is just the expected wait per light (20 seconds) times the number of lights remaining.

We can write a function to do this calculation:

def wait_time_exp(n_lights, n_wands):
    """Calculate Calvin's total expected wait time on his journey home.

    Args:
        n_lights (int): The number of lights on the journey
        n_wands (int): The number of times Calvin can use his wand

    Returns:
        float: The total expected time spent waiting at lights
    """
    # maximum time per timer
    counter_max = 80

    #### Base cases ####
    # no lights left
    if n_lights <= 0:
        return 0
    # enough wands to switch all lights
    elif n_wands >= n_lights:
        return 0
    # no wands left
    elif n_wands <= 0:
        return n_lights * counter_max / 4

    #### Recursion ####
    # cutoff for the number of lights we expect to wait at
    n = n_lights-n_wands
    cutoff = counter_max * (1 - (2/(n+1))*(1 - 1/(2**(n+1))))

    # initialize 3 scenarios
    probs = np.zeros(3)
    waits = np.zeros(3)

    # scenario 0: green light
    probs[0] = 0.5
    waits[0] = wait_time_exp(n_lights-1, n_wands)

    # scenario 1: red light + wait
    probs[1] = 0.5*cutoff/counter_max
    waits[1] = cutoff/2 + waits[0]

    # scenario 2: red light + use a wand
    probs[2] = 0.5*(1 - cutoff/counter_max)
    waits[2] = wait_time_exp(n_lights-1, n_wands-1)

    # return weighted sum of scenarios
    return (probs*waits).sum()

And finally we finish off with some art to confirm that the function is behaving as we expect it to.

# set up variables
n_lights = 20
n_wands = 20

lights = np.arange(n_lights+1)
wands = np.arange(n_wands+1)

# initialize waiting times
times = np.zeros((n_lights+1, n_wands+1,))

# calculate waiting times
for n in lights:
    for w in wands:
        times[n,w] = wait_time_exp(n,w)

# plot the waiting times as a heatmap
plt.figure(figsize=(10, 8,)) 
plt.pcolor(times.T, cmap='jet', linewidth=0.25, edgecolor='w')
plt.title('Total expected waiting time on Calvin\'s walk home')
plt.xlabel('Number of lights'); plt.ylabel('Number of wand uses')
plt.xticks(lights+0.5, lights); plt.yticks(wands+0.5, wands)
plt.colorbar(label='Time (seconds)');

png

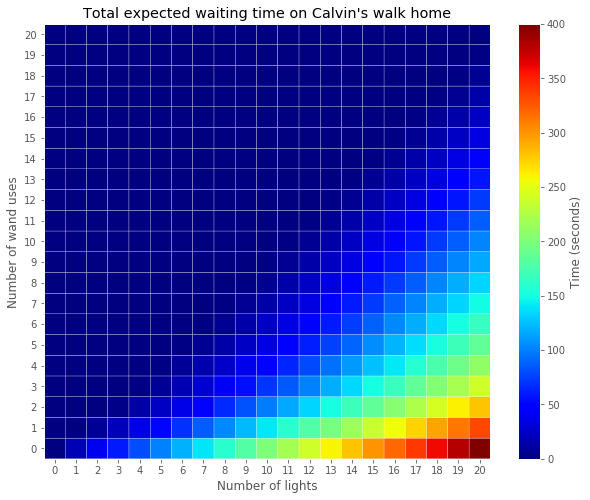
With the problem thoroughly solved, I can finally sleep at night again.